Модели расчета оптимальных режимов эксплуатации стад рыб

Вторая задача, решение которой связано с использованием ЭВМ - это определение такого режима эксплуатации промыслового стада, при котором удастся получить максимум продукции. Это может быть достигнуто путем правильного: 1) подбора возрастного и полового состава уловов, 2) географического размещения промысла, 3) сезонного графика вылова (Никольский, 1958а). Последние два вопроса могут быть успешно решены и без сложных математических расчетов. Что же касается подбора оптимальной возрастной и половой структуры улова, то это требует сложных расчетов и получение необходимых данных может быть значительно упрощено путем математического моделирования и использования ЭВМ. При промысле, базирующемся на половозрелом стаде, а это обязательное условие для рациональной эксплуатации большинства видов промысловых рыб, задача сводится к определению такой величины, при которой взрослое стадо (St) может дать максимальную величину общей смертности, т. е. требуется найти отношение убыль - стадо при таком режиме, когда обеспечивается максимум величины убыли (в весовом выражении). Этот вопрос не является новым в экологической литературе. Подробный разбор истории математического моделирования режима эксплуатации промысловых организмов сделан Уаттом (Watt, 1962).

В общей форме, видимо, правильно уравнение, предложенное Уаттом (Watt, 1962; 1971),

где

G_t+1 - максимальный улов за определенный год;

P_t+1 - биомасса популяции;

P_(min)t+1 - минимальная биомасса популяции, необходимая для воспроизводства следующего максимального улова.

В решении этого уравнения наибольшую трудность представляет определение структуры изымаемой и оставляемой частей популяции, обеспечивающих максимальный улов данного и будущих годов. В этом отношении особое значение имеет расчет наиболее продуктивного возрастного состава оставляемой части популяции и возрастного состава изымаемой части популяции, при которой обеспечивается максимальная продуктивность, т. е. максимальные уловы наиболее высокого качества. В решении второй части вопроса кое-что уже сделано отечественными исследователями (Бервальд, 1956; Бердичевский, 1964, и др.); что же касается первой части вопроса, то в этом отношении исследований еще крайне мало. Естественно, что для организмов с разной продолжительностью жизни характер расчетных уравнений будет несколько различным. По Уатту (1962), простейшая расшифровка вышеприведенного уравнения выглядит так:

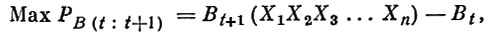(29)

где:

P_B(t:t+1) - продуктивность биомассы за период от t до t + 1;

B_t - биомасса за время t;

B_t+1(X₁X₂...X_n)- биомасса ко времени t + 1 как функция количественных переменных X₁...X_n, определяющих продуктивность биомассы за период времени от t до t + 1.

Основная трудность в решении этого, как мне представляется, в общем близкого к истине уравнения - это определение оптимальных величин биомасс отдельных возрастных групп. Кроме того, вызывает сомнение принятие постоянной величины того "гарантийного минимума" популяции, который должен оставаться для обеспечения воспроизводства. Несомненно^ что этот "гарантийный минимум" должен меняться как по количеству, так и по структуре в связи с периодическими и непериодическими изменениями условий жизни. Познание закономерностей самонастройки популяции в этом отношении имеет важнейшее значение.

В. В. Меншуткин (1964), исследуя построенную мною модель популяции, даже на этой примитивной модели показал полную возможность расчета оптимального режима эксплуатации рыб, как с длительным, так и с коротким жизненным циклом. Как видно из приводимой диаграммы (рис. 108), заимствованной у В. В. Меншуткина (1964), обращает на себя внимание резко очертанный максимум вылова при интенсивности рыболовства F=0,4, не совпадающий с максимальными интенсивностями рыболовства. Существование такого максимума наглядно показывает реальность задачи-нахождения оптимальных режимов рыболовства не только для популяции с длительным жизненным циклом и мало изменяющимся пополнением, но и для популяций рыб с относительно малой продолжительностью жизни и существенной связью между числом производителей и численностью потомства (Меншуткин, 1964).

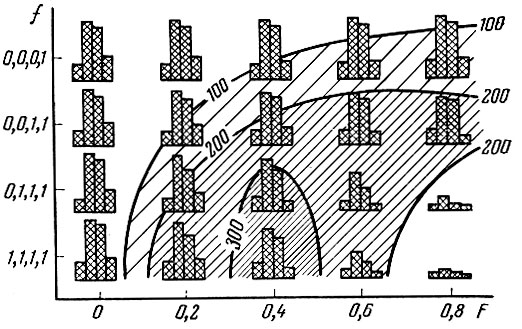
Рис. 108. Изоплетная диаграмма вылова для модели Никольского 0,0,0,1 1960-1961 гг. с указанием равновесных структур популяции (по Меншуткину, 1964): F - интенсивность рыболовства; f - селективность рыболовства в отношении возрастных групп. Столбики - возрастная структура популяции. В правом нижнем углу - режимы 'перелова'; в левом верхнем углу и по всему ряду селективность (f, 0, 0, 0, 1) - режимы 'недолова'. Интенсивная штриховка - максимальный вылов

Мне представляется, что при расчете структуры изымаемой части стада необходимо учитывать следующие данные:

1) прирост массы особей на каждом году жизни;

2) убыль от естественных причин у каждой возрастной группы;

3) качество половых продуктов, производимых особями разного возраста;

4) необходимое соотношение полов для наиболее эффективного воспроизводства стада.

В качестве материала для расчетов должна быть принята прогнозированная структура нерестового стада, исходя из которой и следует вести расчет оптимальной возрастной и половой структуры улова. При этом необходимо принимать во внимание взаимное влияние смежных возрастных групп на особей, слагающих эти смежные поколения (Поляков, 1962).

В итоге должна быть спроектирована такая структура изымаемой части популяции, при изъятии которой из стада обеспечивалось бы получение максимальной величины улова (по массе) и нерестовая популяция сохраняла бы полностью свои воспроизводительные свойства. Естественно, что при этом должны учитываться и величина, и структура будущего пополнения нерестового стада.

В. В. Меншуткиным (1966) предложена и определенная математическая модель оптимальной "стратегии рыболовства", учитывающая, в отличие от ранее предлагавшихся моделей (Баранов, 1961; Beverton a. Holt, 1957), изменчивость и природных условий водоема. Таким образом, может быть получена совокупность предписаний о режиме эксплуатации промыслового вида, выдаваемых органом, регулирующим рыболовство. Однако в большинстве водоемов приходится решать задачу оптимизации эксплуатации не отдельной изолированной популяции, а группы популяций разных видов. В этом плане несомненный интерес представляет модель оптимального вылова при совместной эксплуатации популяций нескольких видов, разработанная Пауликом, Хурстоном и Ларкиным (Paulik, Hourston and Larkin, 1967). Эти авторы установили, при каких условиях такая многовидовая группировка может давать наибольшие устойчивые уловы.

В. В. Меншуткин (1971) показал, что при использовании моделирования и ЭВМ возможен анализ экологической системы водоема, участвующей в создании рыбной продукции как единой системы. Математическая модель этой системы, реализованная на цифровой ЭВМ, может способствовать оптимизации эксплуатации экосистемы водоема как единого целого. В дальнейшем подобный анализ будет способствовать и разработке методов повышения продуктивности экосистем водоемов, выявляя "узкие места" в трофических связях и в воспроизводстве промысловых организмов и их кормовых объектов.