
Биологические основы построения математических моделей
Первая попытка моделирования процесса динамики стада рыбы и построения модели рационального рыболовства была осуществлена в 1915 г. экономистом В. А. Кевдиным (1915). Кевдин исходил из следующих положений: в не облавливаемом водоеме существует подвижное равновесие между рыбными ресурсами и кормовой базой (которую он ошибочно именовал планктоном); величина кормовой базы и рыбных ресурсов в не облавливаемом водоеме суть относительно постоянные величины т. е., по Кевдину,
П = kР
где:
П - производительная мощность кормовой базы;
Р - рыбные ресурсы.
При изъятии человеком части рыбных ресурсов освобождается кормовая база (обозначаемая Кевдиным буквой С), производительная мощность которой позволяет получить дополнительный полезный прирост рыб (А). При рациональном рыбном хозяйстве улов (Y) должен соответствовать полезному приросту, а последний соответствовать производительной мощи кормовой базы. Таким образом, при рациональном рыбном хозяйстве, по Кевдину, А = С и С = Y, В основу как этой, так и большинства других моделей кладется анализ взаимоотношений пищи и потребителя или хищника и жертвы. Исходя из представления о постоянном перенаселений водоемов молодью или о решающем значении гибели на ранних этапах онтогенеза (не зависящей от качества и количества молоди), закономерную связь родительского стада и пополнения обычно отрицают. Если же и признается прямая связь родительского стада и потомства R = f(St), то эта связь характеризуется постоянной величиной.
В первых моделях (Кевдин, Баранов и многие др.) принималось, что кормовая база изменяется только под влиянием выедания рыбами и что между кормовой базой и стадом рыбы существует прямая количественная связь. Первой моделью, основанной на прямой количественной связи пища - потребитель, был предложенный Альмом (Aim, 1924) F/B коэффициент (Benthos fischerei production koeffizient). Из моделей последнего времени к этой группе надо отнести построения Г. К. Ижевского (1961), основанные на связи обеспеченности пищей и численности, и А. Е. Антонова (1962) о связи режима сезона нагула и численности стада промысловой рыбы.
Вторая, пожалуй, наиболее многочисленная группа математических моделей динамики популяций основана на анализе связи хищник - жертва, включая в понятие хищника и вылов. При этом в большинстве случаев естественная смертность принималась за постоянную величину.
Таким образом, большинство моделей было основано на представлении о стабильности кормовой базы и пополнения, т. е. неограниченности числа мальков, из которых выживает лишь столько, сколько могут использовать корм, остающийся от погибающих в результате вылова рыб старших поколений. Величина естественной смертности принималась стабильной. Единственной переменной оказывался вылов. На этом принципе в той или иной степени основаны и модель Росса (1910), и модель Ф. И. Баранова (1918), и модель Лотка - Вольтерра (Lotka, 1925; Volterra, 1926) и ее модификации Г. Ф. Гаузе (1933), А. Н. Колмогоровым (Kolmogoroif, 1936), Грэмом (1939), М. Шефером (1957), Дои (1959, 1962) и многими другими. При этом принималось, что взаимосвязь хищника и жертвы осуществляется по линии отрицательной обратной связи (Малиновский, 1960)
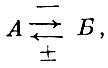 (22)
(22)где:
А - хищник;
Б - жертва,
т. е. жертва улучшает условия жизни хищника, а хищник угнетает жертву. Такого рода связь при запаздывании реакции хищника путем увеличения его численности при увеличении численности жертвы приводит, по мнению А. Н. Колмогорова (1936), к регулярным незатухающим колебаниям как численности жертвы, так и численности хищника.
Однако на самом деле характер взаимодействия хищника и жертвы много сложнее. Связь хищника и жертвы так же, как и связь пища - потребитель, где исследуемая нами рыба выступает уже в роли потребителя, идет не по схеме (22), а по схеме плюс минус взаимодействие в обеих сторонах связи
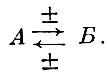 (23)
(23)Хищник, поедая жертву и сокращая ее численность (действие минус)г в то же время создает более благоприятные условия жизни и ускоряет темп воспроизводства оставшейся части жертвы, разрежая ее стадо (действие плюс). В свою очередь жертва, обеспечивая увеличение численности хищника (действие плюс), при сокращении ее численности затормаживает темп воспроизводства хищника, вследствие чего сокращается численность последнего, а в случае рыболовства - снижается величина уловов.
Необходимо учитывать, что усиление воздействия хищников сказывается на жертве с некоторым запозданием, которое бывает меньше в отрицательном случае (непосредственном выедании) и больше в положительном случае, путем увеличения темпа воспроизводства. То же имеет место и в отношении хищника. При этом запаздывание изменения темпа воспроизводства у жертвы - рыб, как правило, с более коротким жизненным циклом и ранней половой зрелостью - оказывается меньшим, чем у хищника - видов с более длительным жизненным циклом и более поздним возрастом наступления половой зрелости. Это не учитывалось при конструировании математических моделей, основанных на схеме Лотка - Вольтерра. Наряду с другими ошибками это и привело к неудаче при использовании таких моделей для работы на ЭВМ . Надо также иметь в виду, что двучленная замкнутая система (23), т. е. продуцент ↔ консумент первого порядка, в природе встречается исключительно редко. В отношении же промысловых рыб мы, как правило, имеем дело с трехчленными пищевыми цепями (24), так называемым триотрофом, по терминологии Б. П. Мантейфеля (1961), где средний член связан прямыми приспособительными связями с крайними. Обычно же число членов в пищевой цепи, в которой участвует промысловый вид, оказывается еще большим
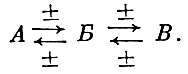 (24)
(24)Эти взаимозависимые цепи (минимум трехчленные), состоящие из взаимосвязанных двучленов, не представляют собой полностью замкнутой системы. Они находятся во взаимодействии со многими различными внешними факторами. Сложность пищевых отношений рыб хорошо показана исследованиями . Е. В. Боруцкого (1960), Н. С. Гаевской (1955), Г. С. Карзинкина (1952), Б. П. Мантейфеля (1961), А. А. Шорыгина (1952) и др. Эта сложная система взаимосвязей далеко не всегда может быть выражена прямыми количественными отношениями. В системе пищевых отношений могут иметь место и воздействия тех факторов или градиентов факторов, к которым виды, слагающие систему триотрофа, не приспособлены, например сильные штормы, заморы и т. п., создающие нарушения, "помехи" в системах пищевых взаимосвязей. Значение "помех" в системах взаимосвязей потребитель ↔ потребляемое, как правило, возрастает в направлении от биологического центра ареала вида к его краю.
Эти сложные отношения, возникающие на почве питания, на практике приводят к тому, что обычно об обеспеченности пищей популяции как мирной, так и хищной рыбы, т. е. о динамике триотрофа, значительно точнее удается судить не по изменению кормовой базы, а по изменению биологических показателей кормящейся популяции. Изменения же кормовой базы могут служить лишь дополнительным показателем для суждения об изменениях обеспеченности популяции пищей. Из этого, конечно, не следует, что в качестве одного из исходных материалов не должны использоваться данные о динамике кормовой базы. Сбор таких данных необходим, но только это должны быть данные, действительно характеризующие кормовую базу, а не осредненные биомассы смеси из кормовых и не потребляемых рыбами в пищу организмов.
Третий тип моделей основан на наличии определенной связи между численностью родительского стада и потомства. Первоначально модели этого типа базировались на представлении об отсутствии компенсаторных механизмов, однако основная масса их учитывает наличие определенных механизмов, регулирующих численность пополнения в относительном соответствии с численностью родительского стада. Подробный обзор этого типа моделей дан В. Е. Риккером (Ricker, 1970) и в последнее время П. Ларкиным (Larkin, 1973).
Наконец, четвертая группа моделей, куда может быть отнесена, например, модель Рессела (Rüssel, 1942), выделяется нами в известной степени условно, так как хотя в формуле, определяющей динамику популяции, фигурирует несколько величин, но, как правило, все, кроме одной, системы связей принимаются постоянными и анализируется лишь одна пара взаимозависимых переменных.
Таким образом, до последнего времени при моделировании динамики популяций рыб исследователи обычно исходили из схемы, показанной на рис. 106, т. е. все отношения принимались постоянными, кроме отношения хищник - жертва.
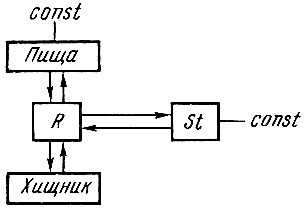
Рис. 106. Схема взаимоотношений родителей - потомства и пищевых связей в триотрофе при наличии одного переменного: R - пополнение; St - родительское стадо
Однако многие исследователи отдавали себе отчет в том, что убыль и пополнение - это взаимосвязанные процессы, это как бы система взаимозависимых переменных, находящихся и под воздействием ряда внешних случайных факторов. Как правильно отметили Хемпель и Зараге (Hempel a. Sahrhage, 1961), наличие нескольких взаимосвязанных переменных "мешало" исследователям в конструировании математических моделей, вследствие чего "для удобства работы" принималась стабильность всех взаимосвязанных членов, кроме одного. Это упрощало моделирование, но приводило к ошибочным результатам. Не случайно поэтому в последние годы раздается все больше голосов в пользу того, что для получения представления об изменениях, происходящих в популяции, можно базироваться на тех ее признаках, которые обеспечивают ее самонастройку на определенный режим существования. Эти высказывания основываются на представлении, что популяция рыб, как и других организмов, представляет собой саморегулирующуюся систему, самонастраивающуюся на определенный режим при помощи комплекса приспособлений, направленных на обеспечение определенной сбалансированности пополнения и убыли.
Механизм этой регуляции осуществляется через изменение обеспеченности пищей - хода обмена - и связанных с нею качественно-количественных свойств популяции: плодовитости, качества половых продуктов, роста, темпа созревания, жирности, изменчивости признаков и свойств и др. Родительское стадо как бы настраивается при помощи своих регуляторных приспособлений на определенную интенсивность воспроизводства применительно к определенным условиям жизни. Естественно, возможности этой "настройки" не безграничны. Темп роста, время полового созревания и другие свойства, связанные с воспроизводством, у особей разных видов рыб могут меняться в разной степени и далеко не безгранично.
Улучшение обеспеченности пищей не может безгранично влиять на изменение темпа роста. Известно много примеров (Никольский, 19536; Крыхтин и Смирнов*, 1962; Матисен, 1962), когда регуляторные механизмы популяции нарушались.
* (Обзор регуляторных механизмов у популяций рыб см. у Никольского, 1960.)
Здесь мы рассматриваем лишь те случаи, когда регуляторные механизмы у популяций работают нормально. Эти представления о популяции как о самонастраивающейся системе в последнее время развиваются очень многими отечественными и зарубежными исследователями. Делаются попытки на основании анализа изменения регуляторных механизмов выявить направление и величину изменений ее численности (Никольский, 1950, и др.; Beverton, 1953; Le Cren, 1962, и др.; Риккер, 1957; Шефер, 1957)1.
Схематически систему связей, определяющих ход процесса динамики популяции, можно изобразить в следующем виде (рис. 107).
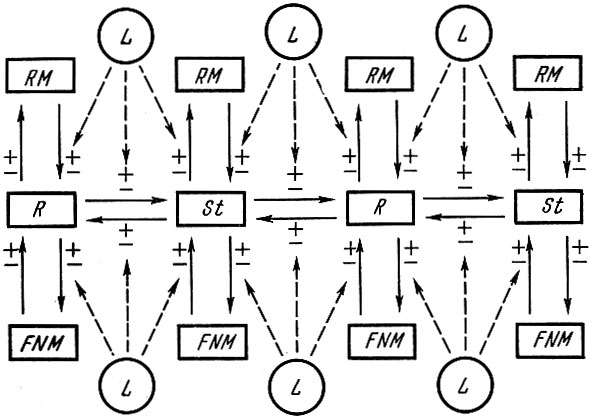
Рис. 107. Схема системы связей, определяющих ход процесса динамики популяции: R - пополнение; St - стадо; RM - обеспеченность пищей; FNM - смертность (промысловая и от естественных причин); L - случайные, часто летальные изменения среды
Конечно, это грубая схема. Пополнение, как и нерестовое стадо, представляет собой систему взаимовлияющих друг на друга поколений, т. е. R=R1 ↔R2↔R3↔R4, так же как и St↔St3↔St4↔St5↔St6.T. д. При этом характер взаимодействия как разных поколений в пополнении, так и разных поколений в нерестовом стаде будет различным. Характер взаимодействия будет определяться как численностью и физиологическим состоянием особей в поколениях, так и теми условиями, в которых они существуют.
Обычно чем сильнее расходятся в росте рыбы разных поколений, чем разобщенней их места нагула и различнее состав пищи, тем это взаимовлияние будет слабее.
Нас интересует в первую очередь определение величины стада и пополнения. Следовательно, нам необходимо создать систему уравнений, отражающих намеченную схему взаимозависимостей.
Математическое моделирование отношений хищник - жертва и потребитель - потребляемое, т. е. так называемого триотрофа, если не допускать чрезмерного упрощения, как это ранее делалось, очень сложно. Оно требует учета сложнейшей системы отношений хищника и жертвы, включающих способы защиты, наличие убежищ и другие формы доступности и т. д. Если в эксперименте иногда удается промоделировать отдельные звенья этой системы отношений (Ивлев, 1955), то в природной обстановке сделать это с необходимой для практики точностью, как правило, невозможно. Поэтому, несомненно, гораздо легче и надежнее оценивать взаимосвязи с пищей и хищниками, т. е. процессы, происходящие в триотрофе, по изменениям биологических показателей как родительского стада, так и пополнения, по изменению тех приспособительных механизмов, которыми популяция реагирует на изменение обеспеченности пищей.
Путем анализа изменений биологических показателей популяции удается уловить несравненно более тонкие изменения в условиях ее существования, чем путем непосредственного анализа динамики этих условий. Я хочу быть понятым верно. Я не отрицаю необходимости осуществлять анализ динамики условий жизни популяции, но более надежным критерием изменения условий часто является анализ изменения самой популяции (т. е. по результирующей), чем этих условий, которые обычно воздействуют на популяцию в сложной и трудно учитываемой взаимосвязи с многими другими факторами.
Важнейшей системой связей, определяющей динамику популяции, является связь стада и пополнения. Эта связь значительно сложнее прямой количественной связи. Во многих случаях так же, как и во взаимоотношениях хищника и жертвы, потребителя и пищи, не удается наблюдать однозначной количественной зависимости между численностью стада и пополнением, но это, конечно, отнюдь не значит, что пополнение не находится во взаимной связи с родительским стадом. Родительское стадо условиями жизни как бы настраивается на воспроизводство определенного количества потомства определенного качественного состава. Поскольку эта "настройка" осуществляется автоматически, то "заданное" в результате изменения условий жизни и в первую очередь изменений в системе триотрофа не всегда приводит к ожидаемому. Таким образом, нам представляется, что в основу математического моделирования динамики популяций должно быть положено выражение
R = f(St), (25)
объединяющее систему уравнений, раскрывающих эту взаимозависимость на ее отдельных этапах. Может быть, правильнее оценивать эту зависимость не как функциональную, подчиняющуюся вышеприведенной формуле, а как корреляционную (Опарин, 1958), выражаемую зависимостью
R=σr(St), (26)
Эта формула исходит из наличия не только основной связи, но и дополнительных взаимозависимостей. Однако это не означает, что в данном случае имеется односторонняя случайная связь. Это уравнение тоже отражает приспособительную взаимосвязь родительского стада и потомства, но с включением и внешних случайных причин и изменений в системе триотрофа.
Вероятно эту зависимость лучше записать как
R = f(StL), (27)
при этом изменения в системе триотрофа, отражающиеся на воспроизводительных свойствах нерестового стада, учтутся его показателями, а случайные отношения будут отражаться через изменения L.
По качественным и количественным показателям родительского стада можно с достаточной точностью предсказать численность и жизнестойкость пополнения. Сведения для количественной характеристики нерестового стада накоплены нашей наукой в большом объеме, и методика их получения разработана вполне удовлетворительно. Необходимы только большая стандартизация их сбора и обработки и ежегодный сбор по определенной программе. Столь же важно упорядочить рыболовную статистику и в первую очередь статистику уловов на рыболовное усилие.
Значительно хуже обстоит дело со сбором данных для качественной характеристики нерестового стада и его половых продуктов. Мы еще очень плохо знаем характер связи качества половых продуктов с возрастом производителей при разной обеспеченности пищей. Особенно плохо изучены закономерности динамики качества молок и их влияние на качество потомства. На разработку методики получения качественной характеристики родительского стада и его половых продуктов необходимо обратить самое серьезное внимание. Отсутствие этих данных может сильно затормозить внедрение в жизнь прогнозирования урожая с использованием счетно-решающих устройств.
Но нас, естественно, интересует не только численность потомства, дожившего до жизнестойкой стадии, но и ход формирования пополнения нерестового стада. Основными показателями, позволяющими характеризовать этот процесс, несомненно, являются темп роста и изменчивость размерного состава одновозрастных группировок. Г. Д. Поляков (1962) наглядно показал, какое огромное влияние на процесс роста рыб в данном поколении могут оказывать рыбы смежных с исследуемым поколений. Этот момент, несомненно, необходимо учитывать при прогнозировании величины и структуры пополнения нерестового стада.
Важнейшее значение в формировании пополнения, его численности и структуры имеет рост рыб. И, конечно, в математической модели динамики популяции должны отражаться и закономерности роста (Russel, 1942; Beverton a. Holt, 1957; Gulland, 1962; Weatherley, 1972 и др.). Анализируя закономерности роста, нельзя также забывать, что имеется не только связь рост - возраст созревания, но и предельный возраст.
При построении математических моделей особое внимание следует обратить на правильную интерпретацию закономерностей формирования возрастной структуры нерестовой популяции. Возрастная структура популяции - это результат взаимодействия процессов пополнения, роста и убыли (Никольский, 1961; Лапин, 1961). Ее нельзя рассматривать лишь как прямую функцию интенсивности смертности. В трактовке причин изменений возрастного состава и по настоящее время допускаются серьезные ошибки.
Для построения математической модели и прогнозирования структуры нерестовой популяции крайне важно знать также периодичность нереста у повторно нерестующих особей. Г. Н. Монастырский (1940) безусловно был прав, когда в свою модель структуры стада воблы включил и рыб, пропустивших один нерестовый сезон. У многих рыб, например проходных, пропуск нерестового сезона, а иногда и нескольких сезонов - это закономерное явление. У этих рыб вообще не бывает особей, нерестующих ежегодно. Периодичность нереста меняется в связи с изменениями обеспеченности пищей, причем у рыб разного возраста это происходит по-разному.
Характер периодичности нереста специфичен для разных видов и популяций одного и того же вида. По биологическим показателям (упитанность, жирность, прирост длины) популяции можно судить о том, какой процент рыб будет повторно нерестовать в следующем году.
При формировании исходной численности пополнения, естественно, приходится учитывать и те случайные причины, которые иногда, особенно в крайних условиях существования вида, могут очень сильно нарушать формирование пополнения (Ricker, 1954; Gulland, 1964; Yoshichara, 1961). Я имею в виду такие, например, явления, как промерзание нерестилищ у дальневосточных лососей, особенно у летней кеты, или падение уровня рек, вызывающее обсыхание икры многих фитофильных рыб, или штормы, вызывающие массовую гибель икры, а иногда и личинок пелагофильных рыб. Я имею в виду здесь те внешние воздействия, которые оказывают непосредственное влияние на численность пополнения или косвенно влияют через систему триотрофа.
Включение этих случайных воздействий в схему формирования прогноза урожая может быть осуществлено лишь при посредстве гидрометеорологического прогноза и не всегда с необходимой точностью. Часто, но далеко не всегда, эти влияния приходится учитывать постфактум и вводить в виде соответствующих дополнительных поправок.
Для промышленности важен прогноз не только численности пополнения, но и его полового состава. В отношении большинства видов, у которых установлена связь между численностью и половым составом популяции, по численности родительского стада и ходу нереста удается прогнозировать и половую структуру популяции (Макеева и Никольский, 1965). Однако закономерности, которым подчиняются связи численности полового состава популяции, для большинства промысловых рыб еще почти не изучены.
Таким образом, схема прогноза рисуется мне в следующем виде. Основная зависимость, выраженная отношением (26), позволяет, с учетом поправок на случайные причины - "помехи в каналах обратной связи", - по качественным и количественным показателям нерестового стада определить исходную величину пополнения. При этом надо иметь в виду, что корреляции эти нелинейные. На основе данных о росте, его изменчивости, данных о взаимовлиянии смежных поколений и смертности можно прогнозировать величину и структуру пополнения нерестового стада (как пополнения нерестового стада в данном году, формирующегося из созревающих рыб разных годов рождения, так и структуру пополнения, сформировавшегося из рыб данного года рождения и вступающего в нерестовое стадо в течение последовательного ряда лет).
Я специально не останавливаюсь здесь на рассмотрении математической интерпретации и методов определения общей смертности. Нельзя не согласиться с Голландом (1964), что это весьма сложный комплексный вопрос. Необходимо только отметить, что смертность, которая включается в систему триотрофа, может быть во многих случаях оценена и при помощи анализа изменений, происходящих в регуляторных механизмах популяции. Надо также напомнить, что определение общей смертности непосредственно по изменению соотношения возрастных групп в популяции, особенно у рыб со значительными флюктуациями пополнения, может привести к огромным ошибкам и в большинстве случаев едва ли может быть использовано для составления надежных прогнозов.
Прогноз структуры остатка дают на основе знания закономерностей динамики его возрастной структуры и периодичности нереста у рыб, находящихся в разном биологическом состоянии.
Очень важная задача, без решения которой нельзя прогнозировать допустимую величину вылова, - это определение величины изъятия, допускаемого нерестовой популяцией. Известно, что у рыб, созревающих поздно, с большой продолжительностью жизни, у которых пополнение составляет небольшой процент от остатка, изымаемая часть может составлять меньший процент, чем у рыб с коротким жизненным циклом и ранней половой зрелостью. К сожалению, ориентировочное определение этой величины сделано лишь для очень немногих видов рыб (кета, горбуша, навага, судак и некоторые др.). Пока неизвестно, как меняется эта допустимая величина изъятия в пределах одной популяции в связи с изменением ее численности и структуры. Необходимо значительно усилить наши исследования в этом направлении. Величину допустимого изъятия можно определить, зная, какая численность и структура нерестовой популяции необходимы для обеспечения воспроизводства нужного пополнения.
Методика определения допустимой величины изъятия, мне думается, в значительной степени с учетом действия регуляторных механизмов должна базироваться на структурных моделях, предложенных мною в 1960 г. Зная, при каком соотношении величины и структуры пополнения и остатка сохраняется стабильная величина популяции, можно легко определить допустимую величину общей (промысловой+естественной) смертности. Сложным представляется разделение естественной и промысловой смертности. Это очень важная и далеко еще не решенная биологами задача.
Несомненно, что методика определения величины естественной смертности у разных видов рыб будет несколько различной. В отношении одних видов эта задача будет решаться легче, других - труднее, но для решения этой задачи надо интенсивно работать.
При построении рационального хозяйства эксплуатация биологических ресурсов водоема обычно строится на использовании взаимосвязанных друг с другом популяций разных видов. Поэтому возникает необходимость моделирования отдельных сообществ и экосистемы водоема в целом и в первую очередь пищевых отношений, складывающихся в экосистеме водоема.
В простейшем виде это моделирование отношений хищник - жертва и системы триотрофа. Дальнейшее усложнение модели путем ввода в нее нескольких популяций, питающихся частично сходной пищей, и нескольких хищников, частично поедающих сходных жертв, а также вылова, воздействующего на популяции разных видов с разной интенсивностью, позволяет приблизить модель к той реальной обстановке, которая складывается в водоеме.
Применение теории графов для исследования закономерностей пищевых отношений в экосистеме водоема, как показывает первый опыт, видимо, может оказаться плодотворным (Меншуткин, 1971).
|
ПОИСК:
|
© AQUALIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://aqualib.ru/ 'Подводные обитатели - гидробиология'
При использовании материалов сайта активная ссылка обязательна:
http://aqualib.ru/ 'Подводные обитатели - гидробиология'